触碰标题下面一行的“邵勇老师”查看所有文章;触碰“数学教学研究”, 关注本微信公众号(sx100sy)。本公众号内容均由邵勇本人独创,欢迎转发,但未经许可不能转载。特别声明,本人未曾授权任何网站(包含微博)和公众号转载邵勇“数学教学研究”公众号的内容。每周推送两到三篇内容上有份量的数学文章,但在行文上力争做到深入浅出。几分钟便可读完,轻松学数学。
今天介绍一个小游戏。是一个人玩的游戏,可以用黑白围棋子来玩儿。但写出来,我就用A和B来代替黑白棋子。先介绍玩法,过程,然后推广到一般情况。
初始状态:

要求最终A与B对调,规则是:A只许朝右走;若A右侧是空位,可以走入空位;若A右侧不是空位但右侧的右侧是空位,则A可以跳到空位。B走动的规则除方向外其他与A的走法相同。
很显然,第一步可以是三个A中右侧的A向右移入空位,或中间的跳入空位。但跳入的走法不可取,因为之后就进展不下去了。
由于A与B的左右对称性,我们可以只考虑第一步A先走的情况。
所以,第1步之后的状况是:

接下来,只能是三个B中左侧的B向左跳入空位,所以第2步之后的状况是:

然后怎么走?可以把左起第4位(规定从左至右的方格编号为第1、2、3、4、5、6、7位)的A右移到空位中(如下图中上边状况所示),但之后或者第6位的B跳入空位,或者第2位的A跳入空位,但这两种情况之后就没有法子走了(AA和BB并排紧挨着,动弹不了,红框所示),如下图中并排的两种情况所示:

所以第3步不能是第4位的A向右移到空位中。所以,第3步只能是第6位的B向左移进入空位,如下图所示:

显然,下一步即第4步只能是第4位的A向右跳入空位中(因为若第7位的B左移到空位中,就堵死了,没有后续走法了)。所以第4步之后的状况是:

观察上图。若第5位的B左移入空位,则左边四个位中为“AABB”,导致其中的AA动弹不得,所以,这种走法不可取。所以,下一步也就是第5步只能是第2位的A跳入空位中,结果如下:

接下来怎么走?可以第1位的A向右移到空位中,也可以第3位的B向左移到空位中。后者不可取,因为之后的路走不通。为什么走不通,我们仔细分析一下。

上图中红框中的双A和双B都把路堵死了。所以,我们只能把第5步之后的状况中的第1位的A向右移到空位中,所以说,得到第6步后的结果如下:

下面的三步分别是:三个B依次向左跳入空位中,所以第7步、第8步、第9步之后的结果分别是:

接下来的第10步、第11步、第12步都很简单,结果分别如下:
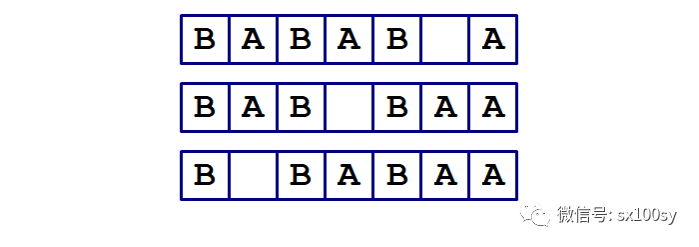
接下来是第13步、第14步、第15步。第15步后便最终完全任务:
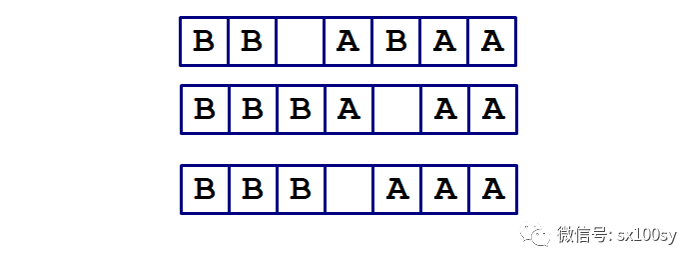
一共15步完全任务,并且,这15步的走法(对第一步走A的情况)都是唯一的。
拓展:如果是左侧有连续的m个“A”,右侧有连续的n个“B”,两者之间仍然是有一个空位,那么,是不是可以做到A整体移到右侧,而B整体移到左侧呢?移动方法是否唯一?若唯一,移动步数是多少?

答案是:可以做到,且移动方法唯一。这个结论不难得出,因为A和B都总是朝着目标方向移动,不允许后退,所以,每一次移动或跳动都是有效的。每个A一定都是向右侧移动了n+1格(先不管是移动到紧挨着的空位中还是跳跃到隔着的空位中),所以m个“A”总共移动了m×(n+1)格;而每个B都是向左侧移动了m+1格,所以n个“B”总共移动了n×(m+1)格。假如说每一次移动都是移动一格,则总步数就是m×(n+1)+n×(m+1)格。但因为所有A都最终挪到了所有B的右侧,而所有B当然也都最终挪到了A的左侧,所以跳跃是不可避免的。并且一定会有不多不少正好m×n次跳跃来完成挪移。这些跳跃都是“一步并作两步”,那么,非跳跃移动(单步)的次数(步数)就是
[m×(n+1)+n×(m+1)] - 2m×n=m+n
再反过来加上跳步m×n步,所以,实际上总的步数就是
m+n+m×n
也可以这样思考:从m×(n+1)+n×(m+1)步(格)中减去“一步并作两步”中多走的n×m格,也可以得到最终结果为:
m×(n+1)+n×(m+1) - m×n
=m×n+m+n
举个例子,左侧有4个“A”,右侧有5个“B”,则把4个“A”全部移动到右侧,把5个“B”全部移动到左侧,一共要挪动4×5+4+5=29步,其中包含“单步”9步,“跳步”20步。
对刚才那个例子,m=3,n=3。所以应该有3+3=6步是单步;有3×3=9步是跳步。您可以从下面的步骤图中数一数是不是这样。(空位移动一位就是单步移动,这里是6个单步;空位移动两位就是跳步,这里是9个跳步。)

注意,上图中,空位走的是“蛇”形。跳步步数(红字所示)分成5组,每组的步数分别为:1,2,3,2,1,它前后对称(两边都是1)。每组跳步之间由单步隔开,且两头都是单步,于是有6个单步。这6个单步的“6”就是3+3(即m+n),而跳步组数为(m+n-1)。所以,我们可以预测3个“A”和4个“B”的情形,这时的m=3,n=4,所以有6(即m+n-1)个跳步组:1,2,3,3,2,1(注意对称性,只可能是这样),这6个组的步数即跳步步数之和等于12;单步步数为m+n=7。所以总步数为12+7=19。








